
Is Skydiving Safer Than Driving?
In the following article I will attempt to answer the question of whether skydiving, in all its forms, is actually safer than driving.
I say ‘attempt’ because the question is sufficiently vague to allow multiple interpretations, and statistics is as much an art as it is a science. We will definitely come to a conclusion, but the flavour of that conclusion is determined by assumptions and choices made by the investigator.
Data, after all, is an abstraction; an incomplete set of measurements taken to try and capture some very complicated reality – a reality that usually has too many variables to conceive, let alone document.
Anybody who wishes to use this partial information to make a sweeping generalisation is going to have to bridge a few gaps, here and there.
This is why it’s important to review the whole of an investigation and not just the summary; you need to ensure that you agree with the liberties and leaps taken by all those involved at every step (I will try to underline and bolden any assumptions I make).
It also gives you a more comprehensive overview of the claims being made so that you can see the truth – the legitimate mathematical machinery, if you will – before it is ham-fistedly translated into sound-bites for the masses.
Now, before I launch into the actual analysis, I have one final preamble to make.
Mainly, why is it that you should listen to me – the distinguished Dr Rush – over other bloggers on the web?
The simple answer to this is: you shouldn’t.
Follow my reasoning and if you agree with it, great – otherwise, don’t. I’m not here to win hearts and minds.
I’m too much of a commitment-phobe to want that sort of responsibility. If you get hurt, I need to be able to say: Hey, that’s all you, buddy! I’m just here to document a line of inquiry; I’m not here to pontificate or promote (contrary to what the hosting site might suggest).
I really have zero emotional investment in skydiving and have never done it. I am too lazy to try new things, and even if I weren’t, I’d be too much of a coward to jump out of a plane.
This is not to say that I can’t comprehend the appeal – the simple serenity of sinking to the ground; weightless, worriless, bereft of any other greater concern than gravity – but I’m much too apathetic allow this to influence me in in any way.
Alright, now we’re ready to start. The first thing to be done is agree a location. Given the level of detail on the British Skydiving website I will stick with Great Britain, comparing skydiving and driving within this country, as opposed to elsewhere in the world.
This is no small point-of-fact, since the safety regulations for parachuting will vary wildly between countries, and so too the number of injuries (if they are even reported) and thus our conclusions.
We also need to decide a timeframe for this investigation, i.e. what years are we going to use to build our assertions on?
Again, I use the BPA as a governing factor in this decision, since they have detailed records for the years 2014 – 2018.
It is a period recent enough to be relevant, but also long to iron out any trends. In the interest of full disclosure, they do have data for the 20 year stretch 1998 – 2018, but I feel any improvements due to contemporary advances in technology (like better equipment, say) would be cancelled out by injuries earlier on in the interval.
If the aim is to get a feel for whether skydiving is safer than driving, now, (and not twenty years ago) then we should not look too far into the past.
But what do we even mean by the term safety? (We’re approaching one of those subjective leaps I flagged earlier in the article) Presumably, we mean resulting in fewer injuries or fatalities. But the controversy then arises as to what we consider an injury.
Given the strict regulations of the BPA, all injuries (no matter how minor) will be recorded if reported.
Consequently, even a negligible affliction like a bruise will be classed as an injury and preserved in the data.
But this causes an inconsistency between the activities of driving a car (note that we will not consider motorcycles, heavy-goods or large-good vehicles) and skydiving, as you are unlikely to report a bruise incurred whilst motoring to work. Indeed, who would you even report it to?
We also have to consider how you quantify a drive. With skydiving, each jump is clearly logged with a beginning and end.
But a drive can’t always be broken down into such isolatable units, nor is each trip archived by some higher authority. I’m not arguing that it should be, just highlighting that we will need to absorb this asymmetry into our investigation.
Bearing the above details in mind, I suggest we measure the safety of driving (a car) by calculating the percentage of driver injuries for each year from 2014 to 2018 (of any severity) and divide through by the respective number of drivers in the country.
This should give a summary statistic that states the average number of accidents per driver, which we can interpret as the chance of being in an accident that year if you were driver.
However, since I don’t have access to how many drivers were in Great Britain, I will instead use the freely available number of registered cars as a surrogate.
I appreciate this might not be wholly accurate as individuals may share cars or own multiple ones, and undoubtedly there are those who don’t register them at all.
But this will just have to do. Statistics is a subject of compromise. We should also stress that by casualties, we are referring just to the driver.
Other people such as pedestrians, passengers and cyclists injured in a road-side accident will be not included in the figure.
This leads to an argument that skydiving is safer than driving when considering its impact on others; in a jump it is unlikely that you will injure anyone other than yourself (although it is possible, of course), but in driving there is a greater spectrum of casualties.
So, using the Annual Reports on Road Casualties and Vehicle Licensing Statistics from the British Government website we obtain the following figures:
| Year | Driver Casualties | Registered Cars (in millions) | (Driver Casualties /Registered Cars) × 100 |
|---|---|---|---|
| 2018 | 65,107 | 31.5 | 0.207% |
| 2017 | 68,688 | 31.291 | 0.220% |
| 2016 | 75,207 | 30.9 | 0.243% |
| 2015 | 76,977 | 30.3 | 0.254% |
| 2014 | 79,297 | 29.6 | 0.268% |
Thus, taking the average of the five years we obtain a value of 0.238%. This is a statistic used to summarize the likelihood of a car-driver suffering an injury (of any severity) over a year, in the interval 2014 to 2018.
We now reproduce the data from the BPA for the total number of injuries per jumps:
| Year | Injuries | Jumps | (Injuries/ Leaps)×100 |
|---|---|---|---|
| 2018 | 145 | 303,882 | 0.0477% |
| 2017 | 143 | 315,290 | 0.0454 |
| 2016 | 168 | 333,955 | 0.0503% |
| 2015 | 154 | 325,254 | 0.0473% |
| 2014 | 170 | 344,607 | 0.0493% |
The average over these five years is 0.048%, meaning that between the years 2014 and 2018, there was a 0.048% chance that a single jump would result in an injury of any severity.
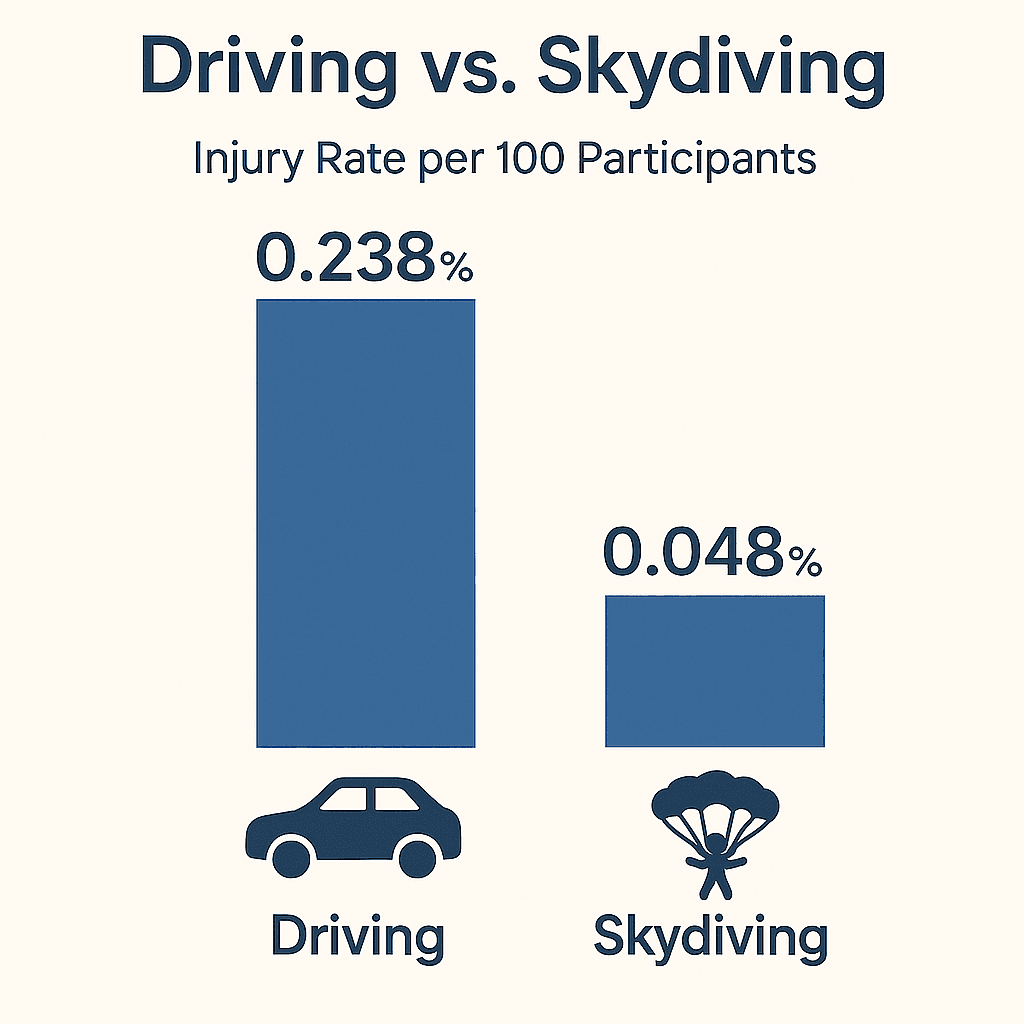
Consequently, since the 0.238% listed for the driver statistic is greater than the
0.048% listed for the skydiving statistic, we see (by the conditions assumed in the
investigation) that the chance of injury for a single jump is less than the chance of injury for driving for a year. Ergo, skydiving is safer than driving.
However, I have to stress the asymmetry here. We are comparing a single jump with driving for a year. Now, if you were to make multiple jumps the risk would, of course, increase. Let’s consider this for a moment: if we assume that injuries between jumps are independent, then the likelihood of any injury after n jumps is (1 - (1- 0.00048)^n). The reasoning behind this is simply that if 0.00048 (we are working with decimals now not percentages, so we have the extra zeros) is the probability of being injured during a jump, then (1- 0.00048) is the probability of not being injured. Consequently, since we have assumed independence, the probability of not being injured after n jumps is (1- 0.00048)^n, and thus the probability of being injured at all after n jumps is 1 - (1- 0.00048)^n. Then, using
logarithms, we see it would take 5 jumps to exceed the risk of driving for a year. Something to chew on.
I should also stress that I have not bothered to distinguish between the different types of skydiving, e.g. tandem, static-line and accelerated free-fall. I’m sure some are riskier than others, but given the broadness of the question I was trying to answer I thought it easiest just to lump them all in together.
These could be topics for later study.
And that’s it. If you’ve made it this far, then thank you for the time and focus. I’m well aware that I write is going to have little impact. Those who already partake in the activity likely find the risk part of the rush and so are indifferent to any statistical analyses that vindicates their hobby – indeed, they might even oppose it. Whilst those who are still undecided and are reading this article to help rally their resolve, I would urge not to go at all.
If you’re a worrywart, like me, who needs to quantify and measure the risk, then maybe freefalling to the ground, with just a sheet strapped to your back, isn’t for you. Stay home and watch Point Break, instead. Man, that’s a good film!